From astronomy to cell biology, the manner in which light propagates in turbid media has been of central importance for many decades. The theory of radiative transfer is widely used to treat this problem by considering the transport of light energy through a random medium and neglecting the wave properties. The basic equation in transport theory is the equation of transfer, for which analytic solutions cannot be obtained for most realistic problems. Solutions are often based on the isotropic diffusion approximation, whose primary assumption is that enough scattering events have occurred so that the diffuse radiation is approximately uniformly scattered in all directions. This approach fails when applied to highly anisotropic scattering media for early times and near boundaries or point-of-entry.

Early-Arriving Photons Traversing a Turbid Medium

We presented a new physical picture for treating energy transport in a multiple scattering medium, which we called "the path integral (PI) approach to photon migration". This picture used the Feynman approach to statistical problems based on his path integral formalism, and provided analytic results to the equation of transfer without the need for making the diffusion approximation. It provided new insights into the propagation of light in a turbid medium by making explicit the most probable path taken by photons as they traverse the medium (Phys. Rev. Lett. 1994).

The probability that a photon will traverse a scattering medium from point \(\mathbf{r}_1\) and \(\mathbf{r}_2\)  in time t can be written as a PI 
$$P(t,\mathbf{r}_1, \mathbf{r}_2)=\int {D\mathbf{r}(t) \times \exp\Bigg[-\frac{1}{2\mu^{\prime}_s} \int^t_0 \ddot{\mathbf{r}} (t)dt\Bigg] \times J[\mathbf{r}(t)]} 
$$ This is an integral over all possible paths from \(\mathbf{r}_1\) and \(\mathbf{r}_2\). The function \(J[\mathbf{r}(t)]\) denotes the density of photon paths, and constrains the photons to propagate at the speed of light at every point of the trajectory.

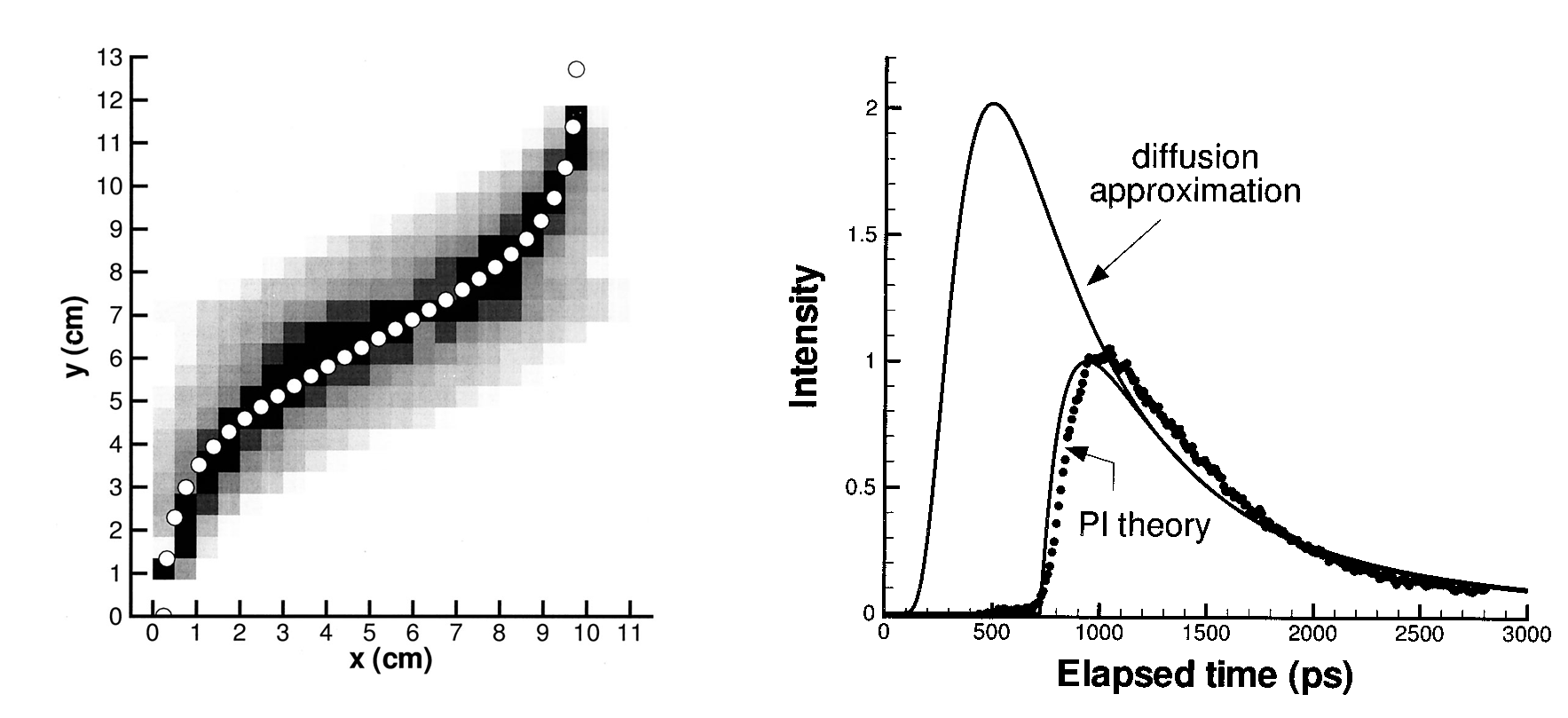
The comparison of the measured intensity with that predicted by the PI theory and the diffusion approximation is shown in the figure. The diffusion approximation does not correctly predict the data at early times; however, the PI theory provides a good fit from the start. In addition, the explicit picture of the most probable photon path given by PI provides beautiful physical insights into the light scattering problem.

Photon Diffusion Near the Point-of-Entry

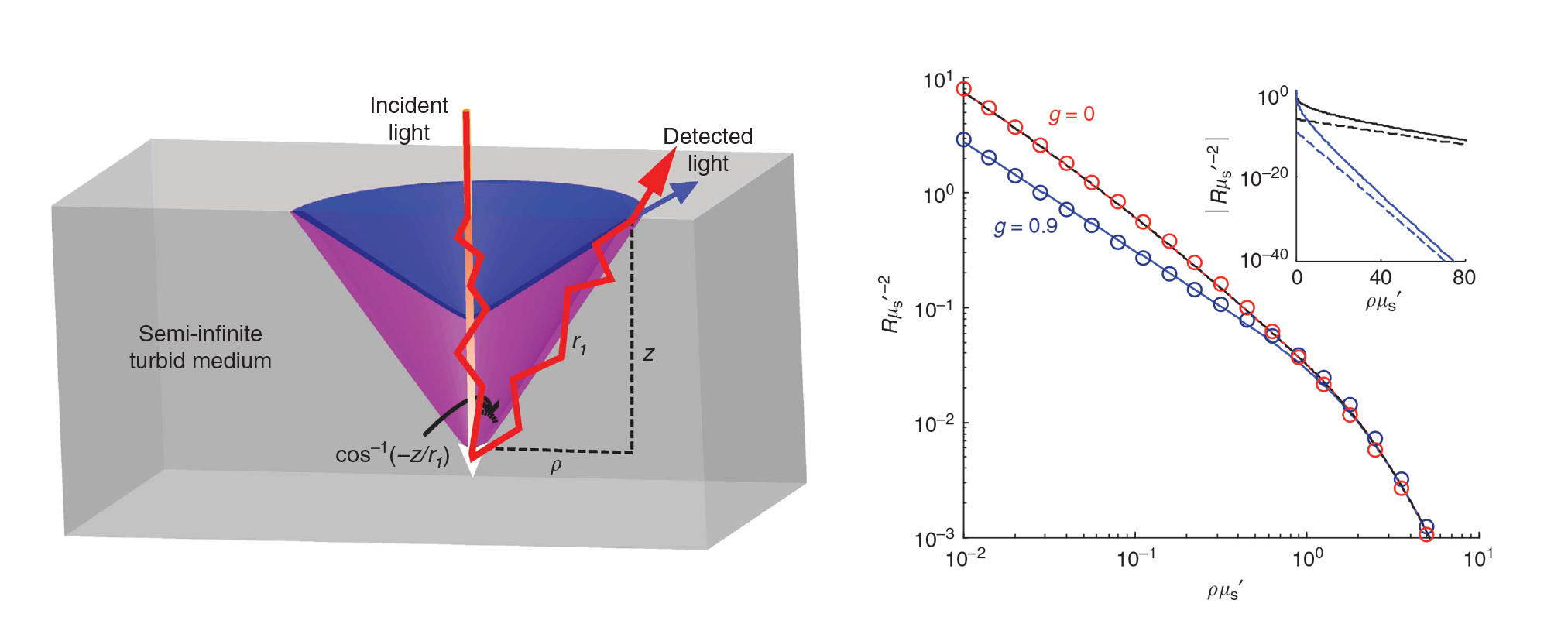
The medium is illuminated with a narrow collimated beam. In addition to unscattered photons, low-angle-scattered photons are also shown. Right panel shows dimensionless reflectance for the phase function corrected (PFC) diffusion theory compared with the Monte Carlo simulations for different anisotropy factors g.We developed a new straightforward analytical theory for light transport in turbid media that addresses the deficiencies of the standard diffusion theory of light transport near the point-of-entry (POE) by accounting for the specific form of the phase function. The diffusion theory is a first-order approximation to the equation of radiative transfer in a sense that scattering in the diffusion approximation is assumed to be either isotropic or near isotropic. However, in the majority of biomedical light scattering applications the phase function, which describes the angular distribution for a single scattering event, is predominantly forward directed. Nevertheless, the transport of light at large distances is still accurately described by the diffusion approximation, because the effects of anisotropic scattering become averaged out over many scattering events. This makes the diffusion approximation a powerful tool for many biomedical applications. However, a large number of biomedical applications require the prediction of radiance near the source or the point-of-entry. Here a more rigorous solution of the radiative transfer equation is needed, either computational (e.g. the Monte Carlo simulation) or analytical. In recent years, several types of perturbation analysis have been introduced in an attempt to improve the performance of the diffusion approximation for biological media near the POE. Each of these methods includes higher-order terms of the scattering phase function in addition to the terms that are normally included in the diffusion approximation. We have developed an accurate method that overcomes this longstanding, unsolved problem in radiative transport. Our phase function corrected (PFC) diffusion theory properly treats anisotropic photon scattering events and correctly predicts the spatially dependent diffuse reflectance of light near the point-of-entry for any arbitrary phase function. We demonstrate that the theory is in excellent agreement with both the experimental results and Monte Carlo simulations for several commonly used phase functions (Nature Commun. 2011).